Risiko
Das üblichste Risikomaß für Finanzinstrumente ist die Streuung, mit welcher ihre periodischen Realrenditen um einen gewissen Bezugswert, den sogenannten Schwerpunkt, verteilt sind. Es wird hier der arithmetische Durchschnitt der Realrenditen als Schwerpunkt ihrer Verteilung betrachtet. Seien nun 
mit t = 1,2,…,T die Realrenditen des Finanzinstruments a in T aufeinanderfolgenden Perioden (z.B. Wochen oder Monaten) und sei 
ihr arithmetischer Durchschnitt, d.h. 
, dann ist die Varianz von a definiert als
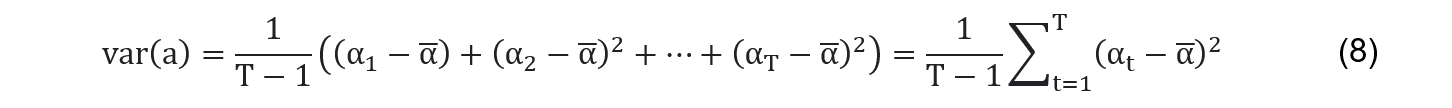
und ist die Volatilität von a definiert als
Risiko von Portfolio ist nicht gewichtete Summe der Risiken seiner einzelnen Bestandteile!
Für das Verständnis der Auswirkung von Diversifikation ist von besonderer Bedeutung, daß das Risiko eines Portfolios im Gegensatz zu seiner Rendite nicht einfach nur eine gewichtete Summe ist:
- Die Rendite eines Portfolios P aus Komponenten a und b, welche jeweils über Gewichtungen in P von wa und wb sowie über Renditen von
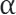und β verfügen, ist die gewichtete Summe dieser Renditen:
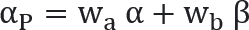
- Die Varianz bzw. das Risiko von Portfolio P ist hingegen nicht nur die gewichtete Summe der Varianzen von a und b, sondern beinhaltet einen zusätzlichen Ausdruck, nämlich die gewichtete Kovarianz der Renditen von a und b, bezeichnet als cov(a,b):
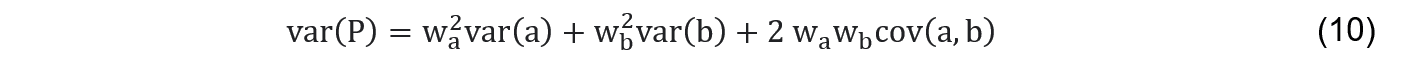
Die Kovarianz ist ein Ausdruck für die Tendenz zweier Variablen, sich in die gleiche Richtung zu bewegen und ist für Portfoliorisiko von fundamentaler Bedeutung:
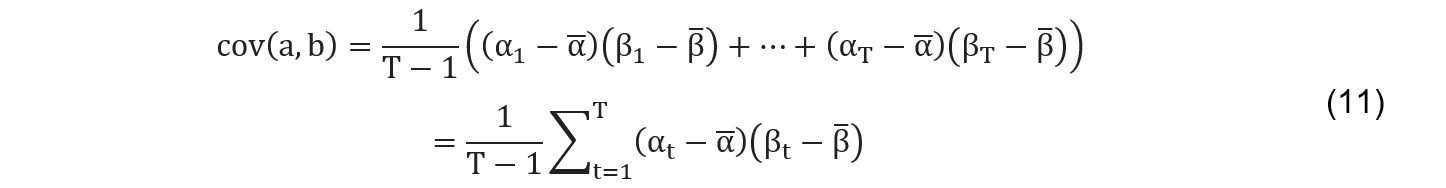
Positive Kovarianz bedeutet, daß die Renditen von a und b insofern in die gleiche Richtung tendieren, als sie in den meisten Perioden über das gleiche Vorzeichen verfügen; es sind also in fast jeder einzelnen Perioden entweder beide Renditen positiv oder beide Renditen negativ. Negative Kovarianz deutet hingegen darauf hin, daß die Renditen von a und b in ungleiche Richtungen tendieren, d.h. in fast jeder einzelnen Periode verschiedene Vorzeichen aufweisen.
Für einen praktischeren Vergleich der Kovarianzen verschiedener Vermögenswerte wird die Kovarianz zu einem Wert zwischen -1 und 1 skaliert, dem sog. Korrelationskoeffizienten, kurz corr; zu diesem Zweck wird die Kovarianz von a und b durch das Produkt ihrer Volatilitäten dividiert:[103]
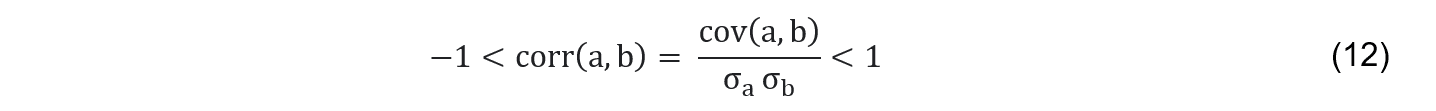
Ein Korrelationskoeffizient von 1 bedeutet, daß die Renditen von a und b perfekt positiv korreliert sind, d.h. in allen Perioden nicht nur das gleiche Vorzeichen, sondern auch genau den gleichen Wert aufweisen. Ein Korrelationskoeffizient von -1 bedeutet hingegen, daß die Renditen von a und b perfekt negativ korreliert sind, d.h. in jeder Periode den gleichen Wert aufweisen, allerdings mit unterschiedlichen Vorzeichen. Bei einem Korrelationskoeffizient von 0 sind a und b unkorreliert, d.h. ihre Renditen haben weder gleichgerichtete noch entgegengesetzte Tendenzen.
Durch einfaches Umformen der Gleichung in (12) und Einsetzen in (10) erhält man bereits jenen Ausdruck des Portfoliorisikos, aus dem mit bloßen Kenntnissen aus der Schulmathematik leicht alle weiteren Schlußfolgerungen abgeleitet werden können:
Wie mit vollständiger Induktion gezeigt werden kann, gilt Gleichung (13) sinngemäß für Portfolios mit einer beliebigen Anzahl von n Bestandteilen. Die Volatilität bzw. das Risiko σP eines Portfolios aus Anlagen a1, a2, …, an mit Gewichtungen w1, w2, …, wn und Volatilitäten σ1, σ2, …, σn ist also:
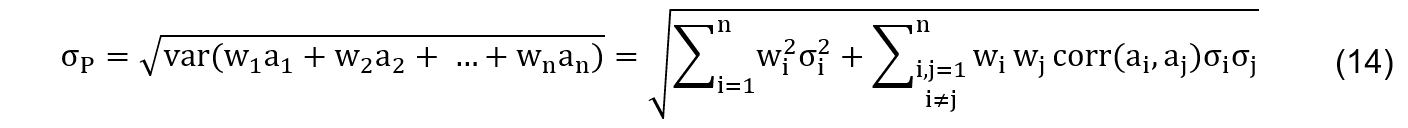
Hoffentlich erwies sich der Inhalt dieser Seite für Sie als nützlich und beantwortete möglichst viele Ihrer Fragen. Wenn Sie weitere Fragen über die Anlegung von Mündelgeld haben, steht Ihnen der Autor Mag. Alexander Giuliani dafür als Sachverständiger und unabhängiger Vermögensberater zur Verfügung.
[103] Die Ungleichung in (12) folgt aus dem mathematischen Satz von Cauchy-Schwarz, wonach für zwei beliebige Vektoren 
gilt: 
. Dabei bezeichnet 
die euklidische Norm, d.h. 
.